Welteroberung: Unterschied zwischen den Versionen
Aus mathespiele
K (1 Version: Import von eigener Seite mathespiele.info) |
K |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
[[Kategorie: Methodische Großform]] | [[Kategorie: Methodische Großform]] | ||
[[Kategorie: 60-90 Minuten]] | [[Kategorie: 60-90 Minuten]] | ||
| + | |||
| + | [[Bild: Welteroberung.png|right|thumb|200px|Welteroberung -Grundspiel]] | ||
| + | |||
== Material == | == Material == | ||
| Zeile 13: | Zeile 16: | ||
== Beschreibung == | == Beschreibung == | ||
| − | * Auf der Karte existieren Kontinente | + | * Auf der Karte existieren Kontinente. Hinter jedem Kontinent verbirgt sich ein Aufgabentyp - je nach Kontinent können unterschiedliche Aufgabentypen thematisiert werden (z. B. Brüche - Prozente - Winkel - Kopfrechnen - Terme - Körper - ...). |
* Die Klasse wird nun in zwei Gruppen eingeteilt. Spieler 1 von Gruppe 1 wählt nun eine Aufgabe. Alle Schüler der Gruppe lösen die Aufgabe. | * Die Klasse wird nun in zwei Gruppen eingeteilt. Spieler 1 von Gruppe 1 wählt nun eine Aufgabe. Alle Schüler der Gruppe lösen die Aufgabe. | ||
* Sobald ein Schüler denkt, die Lösung zu haben, ruft er 'Stopp', dann ist nur noch eine Minute Zeit (Alternativ: Lehrer gibt Zeitbegrenzung vor). | * Sobald ein Schüler denkt, die Lösung zu haben, ruft er 'Stopp', dann ist nur noch eine Minute Zeit (Alternativ: Lehrer gibt Zeitbegrenzung vor). | ||
| Zeile 24: | Zeile 27: | ||
Spannender wird das Spiel, wenn weitere Regeln verwendet werden, bspw.: | Spannender wird das Spiel, wenn weitere Regeln verwendet werden, bspw.: | ||
| − | # Angriff auf | + | # Angriff auf benachbartes Land: Eine Gruppe kann ein benachbartes Land angreifen. Sind dort mehr Mathestreitkräfte vorhanden als im eigenen Land, muss die entsprechende Zahl an Schülern mehr die Lösung der nun gestellten Frage richtig haben. |
# Sonderpunkte, wenn ein ganzer Kontinent von einer Gruppe vereinnahmt ist. | # Sonderpunkte, wenn ein ganzer Kontinent von einer Gruppe vereinnahmt ist. | ||
# Sondermathestreitkräfte, wenn strategische Punkte (Land mit Mathematikhochschule) im Besitz sind (kann Lehrer optional für schwächere Gruppe bereitstellen) | # Sondermathestreitkräfte, wenn strategische Punkte (Land mit Mathematikhochschule) im Besitz sind (kann Lehrer optional für schwächere Gruppe bereitstellen) | ||
# und viele mehr (Verschieben von Mathestreitkräften, Matheexpeditionen, Naturkatastrophen, Schiffsreisen, ...) | # und viele mehr (Verschieben von Mathestreitkräften, Matheexpeditionen, Naturkatastrophen, Schiffsreisen, ...) | ||
| + | |||
== Beispiele == | == Beispiele == | ||
* ab Klassenstufe 5 für alle Themen einsetzbar | * ab Klassenstufe 5 für alle Themen einsetzbar | ||
Aktuelle Version vom 19. Juli 2017, 07:20 Uhr
Inhaltsverzeichnis |
Material
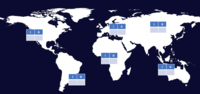
- vorbereitete Kontinent- bzw. Länderkarte (an Tafel, Folie oder über Computer)
- Aufgabenpool
Beschreibung
- Auf der Karte existieren Kontinente. Hinter jedem Kontinent verbirgt sich ein Aufgabentyp - je nach Kontinent können unterschiedliche Aufgabentypen thematisiert werden (z. B. Brüche - Prozente - Winkel - Kopfrechnen - Terme - Körper - ...).
- Die Klasse wird nun in zwei Gruppen eingeteilt. Spieler 1 von Gruppe 1 wählt nun eine Aufgabe. Alle Schüler der Gruppe lösen die Aufgabe.
- Sobald ein Schüler denkt, die Lösung zu haben, ruft er 'Stopp', dann ist nur noch eine Minute Zeit (Alternativ: Lehrer gibt Zeitbegrenzung vor).
- Es erfolgt eine Auswertung: Die Gruppe mit den meisten richtigen Lösungen besetzt das Gebiet.
- Nun werden auf der Karte so viele Striche gemacht, wie Schüler mehr die Lösung richtig hatten.
- Hatte die Gruppe bei der Aufgabe drei richtige Lösungen mehr, erhält sie drei Striche. Man kann sich die Striche als eine Art Mathestreitkraft vorstellen.
- Welche Gruppe hat am Ende die meisten Länder / Kontinente besetzt?
Bemerkung
Spannender wird das Spiel, wenn weitere Regeln verwendet werden, bspw.:
- Angriff auf benachbartes Land: Eine Gruppe kann ein benachbartes Land angreifen. Sind dort mehr Mathestreitkräfte vorhanden als im eigenen Land, muss die entsprechende Zahl an Schülern mehr die Lösung der nun gestellten Frage richtig haben.
- Sonderpunkte, wenn ein ganzer Kontinent von einer Gruppe vereinnahmt ist.
- Sondermathestreitkräfte, wenn strategische Punkte (Land mit Mathematikhochschule) im Besitz sind (kann Lehrer optional für schwächere Gruppe bereitstellen)
- und viele mehr (Verschieben von Mathestreitkräften, Matheexpeditionen, Naturkatastrophen, Schiffsreisen, ...)
Beispiele
- ab Klassenstufe 5 für alle Themen einsetzbar
weitere Informationen
- von Beyer, N. adaptierte Version des Spiels Risiko