Gutschein-Schuldschein-Spiel: Unterschied zwischen den Versionen
Aus mathespiele
K |
K |
||
| Zeile 37: | Zeile 37: | ||
== weitere Informationen == | == weitere Informationen == | ||
| − | * http://mathematik.bildung-rp.de/fileadmin/user_upload/mathematik.bildung-rp.de/Sinus_und_Sinus-Transfer/4.1_OA_7__pdf_/3.3_Gib-Nimm-Spiel.pdf | + | * Bicker, U., Ossmann, H.: Aufgabeneinheit 3: Gib-Nimm-Spiel. Abruf am 28.10.2014 unter: http://mathematik.bildung-rp.de/fileadmin/user_upload/mathematik.bildung-rp.de/Sinus_und_Sinus-Transfer/4.1_OA_7__pdf_/3.3_Gib-Nimm-Spiel.pdf |
| − | + | * Mohler, M.: Die negativen Zahlen im Schulunterricht. Einführung, Übungsbeispiele und Abstraktionshilfen. Abruf am 28.10.2014 unter: http://jones.math.unibas.ch/~zehrtc/institut/vorlesungen/hs09/sla/MMohler.pdf | |
| − | + | * Tischler, L, Hänel, M., Zeh, F.: Von den Bruchzahlen zu den rationalen Zahlen. Vortrag. Abruf am 28.10.2014 unter http://didaktik.mathematik.hu-berlin.de/files/bruch_rational_rechenregeln.pdf | |
Version vom 29. Oktober 2014, 09:39 Uhr
Inhaltsverzeichnis |
Material
- Ereigniskarten (oder zwei Würfel: einen mit + und -, einer mit Zahlen)
- Gutscheinkarten (ca. 60)
- Schuldscheinkarten (ca. 60)
- Blatt und Stift für Protokollführung
Beschreibung
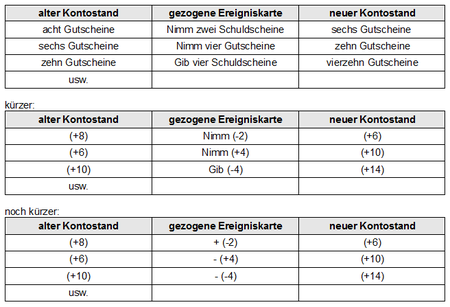
- Es stehen Gutscheine und Schuldscheine zur Verfügung. Ein Gutschein und ein Schuldschein heben sich im Wert auf.
- Zunächst erhält jeder Schüler die gleiche Menge an Gut- und Schuldscheinen (zum Beispiel acht Gutscheine, keine Schuldscheine). Die Ereigniskarten werden gemischt und verdeckt auf den Tisch gelegt.
- Die übrigen Gut- und Schuldscheine liegen griffbereit auf dem Tisch.
- Es wird reihum die oberste Ereigniskarte aufgedeckt und der entsprechende Auftrag ausgeführt.
- Jede Kontobewegung wird protokolliert, siehe Beispielprotokoll (für dieses Protokoll ist die Vereinbarung nötig, dass nach jedem Zug jeder Spieler nur eine Sorte Scheine auf der Hand haben darf)
- Gewonnen hat der Spieler, der am Ende den höchsten Kontostand aufweist.
Bemerkung
- Es bietet sich an, zunächst drei Proberunden zu spielen ohne Protokoll zu führen. Fragestellung: Wie kann herausgefunden werden, wer gewonnen hat?
- Es kann vereinbart werden, dass nach jedem Zug jeder Spieler nur eine Sorte Scheine auf der Hand haben darf (nur Gut- oder nur Schuldscheine). Es muss daher entsprechend mit der Bank getauscht werden (Nulloperation).
- Es kann nach Runden (zum Beispiel zehn Runden), nach Zeit (zehn Minuten) oder bis zum Ende des Ereigniskartenstapels gespielt werden.
- Die Protokollführung kann im Laufe des Spiels gekürzt werden, es bietet sich an, auf den Unterschied von Rechen- und Vorzeichen einzugehen.
- weiterführende Fragestellungen:
- Wie sieht der Kontostand bei zwölf Gut- und zwölf Schuldscheinen aus?
- Was passiert, wenn nicht genügend Gut- oder Schuldscheine vorhanden sind, um eine Anweisung auszuführen? => Statt Schuldscheine abzugeben, kann ich Gutscheine aufnehmen => Aufstellen von Permanenzreihen möglich.
- Weiterführende Beispiele, bei denen die Vorgänge als Rechnung aufgeschrieben werden, sollten sich anschließen.
Beispiele
Eignet sich gut zur Einführung der Addition und Subtraktion rationaler Zahlen in Klassenstufe 7. Es existiert ein Ausschneidebogen.
weitere Informationen
- Bicker, U., Ossmann, H.: Aufgabeneinheit 3: Gib-Nimm-Spiel. Abruf am 28.10.2014 unter: http://mathematik.bildung-rp.de/fileadmin/user_upload/mathematik.bildung-rp.de/Sinus_und_Sinus-Transfer/4.1_OA_7__pdf_/3.3_Gib-Nimm-Spiel.pdf
- Mohler, M.: Die negativen Zahlen im Schulunterricht. Einführung, Übungsbeispiele und Abstraktionshilfen. Abruf am 28.10.2014 unter: http://jones.math.unibas.ch/~zehrtc/institut/vorlesungen/hs09/sla/MMohler.pdf
- Tischler, L, Hänel, M., Zeh, F.: Von den Bruchzahlen zu den rationalen Zahlen. Vortrag. Abruf am 28.10.2014 unter http://didaktik.mathematik.hu-berlin.de/files/bruch_rational_rechenregeln.pdf