Rechen-Stadt-Land-Fluss: Unterschied zwischen den Versionen
Aus mathespiele
(→Beispiele) |
K |
||
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
[[Kategorie: 10-20 Minuten]] | [[Kategorie: 10-20 Minuten]] | ||
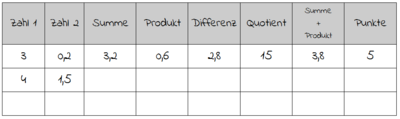
| − | [[Bild: rechen-stadt-land-fluss.png|right|thumb|400px|Rechen-Stadt-Land-Fluss]] | + | [[Bild: rechen-stadt-land-fluss.png|right|thumb|400px|Rechen-Stadt-Land-Fluss für Klassenstufe 6]] |
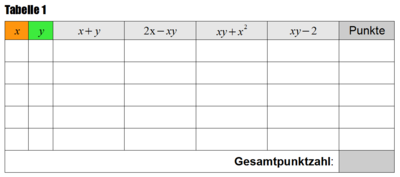
| + | [[Bild: Rechen-stadt-land-fluss-terme.png|right|thumb|400px|Rechen-Stadt-Land-Fluss für Klassenstufe 8 (Terme)]] | ||
== Material == | == Material == | ||
| − | Zettel, Stift, | + | Zettel, Stift, Zahlenkarten oder Würfel |
== Beschreibung == | == Beschreibung == | ||
| Zeile 18: | Zeile 19: | ||
== Bemerkung == | == Bemerkung == | ||
| − | Statt die Zahlen zu würfeln, können auch beliebige Zahlen vorgegeben (oder aus einer vorbereiteten Box gezogen) werden. Dadurch wird auch mit größeren Zahlen gerechnet. Teilweise müssen die vorgegebenen Zahlen geschickt gewählt werden, um einen ganzzahligen Quotienten zu ermöglichen oder im Bereich der positiven rationalen Zahlen zu bleiben. | + | *Statt die Zahlen zu würfeln, können auch beliebige Zahlen vorgegeben (oder aus einer vorbereiteten Box gezogen) werden. Dadurch wird auch mit größeren Zahlen (oder rationalen Zahlen usw.) gerechnet. Teilweise (Klasse 5 und 6) müssen die vorgegebenen Zahlen geschickt gewählt werden, um einen ganzzahligen Quotienten zu ermöglichen oder im Bereich der positiven rationalen Zahlen zu bleiben. |
| + | *Die Lösungen können, wenn vom Lehrer gewünscht, mit dem Taschenrechner verglichen werden. | ||
== Beispiele == | == Beispiele == | ||
| − | Klasse 5: Rechnen mit natürlichen Zahlen | + | * Klasse 5: Rechnen mit natürlichen Zahlen |
| − | + | * Klasse 6: Rechnen mit gebrochenen Zahlen (siehe [[:Datei:Rechen-Stadt-Land-Fluss.pdf| Arbeitsblatt]]) | |
| − | Klasse 6: Rechnen mit gebrochenen Zahlen (siehe [[:Datei: | + | * ab Klasse 7 kann ein beliebtes Term-Stadt-Land-Fluss gespielt werden (siehe [[:Datei:Rechen-Stadt-Land-Fluss-Terme.pdf| Arbeitsblatt]]). |
== weitere Informationen == | == weitere Informationen == | ||
| − | Ferent, U.: Mathe-Spiele für den Unterricht selbst entwickeln. Mit Kopiervorlagen für GS und Sek1. Lehrerselbstverlag: 2010, S. 64-65. | + | * angelehnt an Ferent, U.: Mathe-Spiele für den Unterricht selbst entwickeln. Mit Kopiervorlagen für GS und Sek1. Lehrerselbstverlag: 2010, S. 64-65. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Aktuelle Version vom 28. Oktober 2014, 16:15 Uhr
Inhaltsverzeichnis |
Material
Zettel, Stift, Zahlenkarten oder Würfel
Beschreibung
Es ist zunächst eine Tabelle vorzubereiten (alternativ Arbeitsblatt). In den Tabellenkopf werden nun je nach aktuellem Stoff Rechenanweisungen geschrieben. Dann werden zwei Zahlen vorgegeben (oder gewürfelt / gezogen). Jetzt beginnen alle zu rechnen und zu schreiben. Wer zuerst fertig ist, ruft laut "Stopp". Sofort müssen alle das Schreiben beenden (Alternativen: Lehrer legt Zeitdauer fest / nach dem Stopp noch eine Minute). Der Stopprufer darf dann seine gefundenen Lösungen vortragen. Die anderen Schüler vergleichen ihre Lösungen. Für jede richtige Lösung gibt es einen Punkt. Der schnellste Schüler erhält, wenn seine Lösungen alle richtig sind, einen Zusatzpunkt.
Bemerkung
- Statt die Zahlen zu würfeln, können auch beliebige Zahlen vorgegeben (oder aus einer vorbereiteten Box gezogen) werden. Dadurch wird auch mit größeren Zahlen (oder rationalen Zahlen usw.) gerechnet. Teilweise (Klasse 5 und 6) müssen die vorgegebenen Zahlen geschickt gewählt werden, um einen ganzzahligen Quotienten zu ermöglichen oder im Bereich der positiven rationalen Zahlen zu bleiben.
- Die Lösungen können, wenn vom Lehrer gewünscht, mit dem Taschenrechner verglichen werden.
Beispiele
- Klasse 5: Rechnen mit natürlichen Zahlen
- Klasse 6: Rechnen mit gebrochenen Zahlen (siehe Arbeitsblatt)
- ab Klasse 7 kann ein beliebtes Term-Stadt-Land-Fluss gespielt werden (siehe Arbeitsblatt).
weitere Informationen
- angelehnt an Ferent, U.: Mathe-Spiele für den Unterricht selbst entwickeln. Mit Kopiervorlagen für GS und Sek1. Lehrerselbstverlag: 2010, S. 64-65.